B 2 x 2 = b 2 ( b h a − b) 2 = b a − b ( a − b) 2 h 2 よって、小さな円錐の側面積は、 円錐の側面積の求め方 を使うと、 π × b × b a − b ( a − b) 2 h 2 = π b 2 a − b ( a − b) 2 h 2 同様に、大きな円錐の側面積は、 π × a × a 2 ( x h) 2 = π a × a 2 ( a h a − b) 2 = π a 2 a − b ( a − b) 2 h 2 と 円錐の表面積の求め方の公式 って知ってる? 円錐の半径をr、母線の長さをLとすると、円錐の表面積はつぎのように計算できちゃうんだ。 πr(L+r) 中1 数学 表面積の求め方 表面積の求め方と!円錐の側面積と中心角の簡単な裏ワザをごしょーかい!ページ数少ないです笑 塾で教えてもらいました(((( 学年 中学1年生, 教科書 新編 新しい数学1 東京書籍, 単元 立体の体積と表面積, キーワード 中1,数学,表面積,求め方,まとめ,裏ワザ,簡

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo
円錐の面積の求め方 公式
円錐の面積の求め方 公式-円錐 図のような底面が半径3cmの円で母線の長さが8cmの円錐がある この円錐の展開図を書くときに円錐の側面となるおうぎ形の中心角を求めてください またこのおうぎ形の面積を求めてください ただし円周率はπとします 解き方の説明もあればうれしいです 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし



Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ
四角柱の底面積は「台形の面積」を求めましょう。 四角柱の底面積= (46)÷2×5=25cm 2 円錐の側面積の求め方ですね。 円錐の側面積の求め方 母線×底面の半径×314 確かにこの公式を覚えておけば側面積を即答できるため、圧倒的に有利なのですが、それは覚えていられる間の話。 もし 忘れたり混乱したりすると、求められなくなってA = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径
まずは公式にしたがって円錐の底面積を求めましょう。 底面積 $$\pi \times 3^2=9\pi(cm^2)$$ 次は母線と半径をかけて、側面積を求めます。 側面積 $$8\times 3\times \pi=24\pi(cm^2)$$ 底面積と側面積がそれぞれ求まれば、あとは合計すれば終わり。 表面積円錐の表面積の求め方 😔 今回は、上記の図で言うところのlがわかっていないので、まずはlを求めましょう。 底面の半径と高さから表面積を求める問題 次の問題は、中学3年で学習するを組み合わせて解 《円錐の体積の求め方》 円錐の体積=底面積×高さ÷3なので 答え 2355cm³ 問題② 次の円錐の体積を求めましょう。 (円周率は314とします。) 《円錐の体積の求め方》 円錐の体積=底面積×高さ÷3なので 答え 096cm³ スポンサードリンク 問題③
このことから、おうぎ形の弧の長さと元の円周の長さを比べると 14 ÷ 314 = 3 5 よって、おうぎ形の面積は元の円の面積の 3 5 となり、おうぎ形の面積は 5 × 5 × 314 × 3 5 = 5 × 3 × 314 = 471 c m 2円錐の表面積を求める公式 は、次の通りです。 S = πr(r R) = π ×(底面の半径)× {(底面の半径) (母線の長さ)} S = π r ( r R) = π × (底面の半径) × { (底面の半径) (母線の長さ) } 底面の半径 r、母線の長さ R の円錐 1行目の文字について、S は円錐の表面積、r は底面の円の半径、R は母線の長さを表します。 手っ取り早く円錐の体積を求めるには、この表面積 = 半径 × 半径 × 314 半径 × 母線の長さ × 314




中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル




この問題の円錐の底面積の半径の求め方を教えてください Clear
も円柱の側面積の積み重ねの考え方が適用できるのか. (C) 回転体の体積を求めるときに,円錐台の体積の積み重ねで求めてもよいか.また,円柱 の体積の積み重ねでの考え方とどう違うのか. (D) 回転体の側面積の公式 S f x f x dx b ³ aですが、次の方法で簡単に計算することができます。 円すいの側面積 = 母線 × 半径 × π 5 × 3 × π = 15 π c m 2 問題表面積を求めなさい。 表面積 = 側面積 底面積 底面積は 9 π c m 2 、側面積は 15 π c m 2 よって、表面積は 15 π 9 π = 24 π c m 2円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
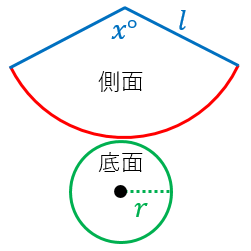



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学
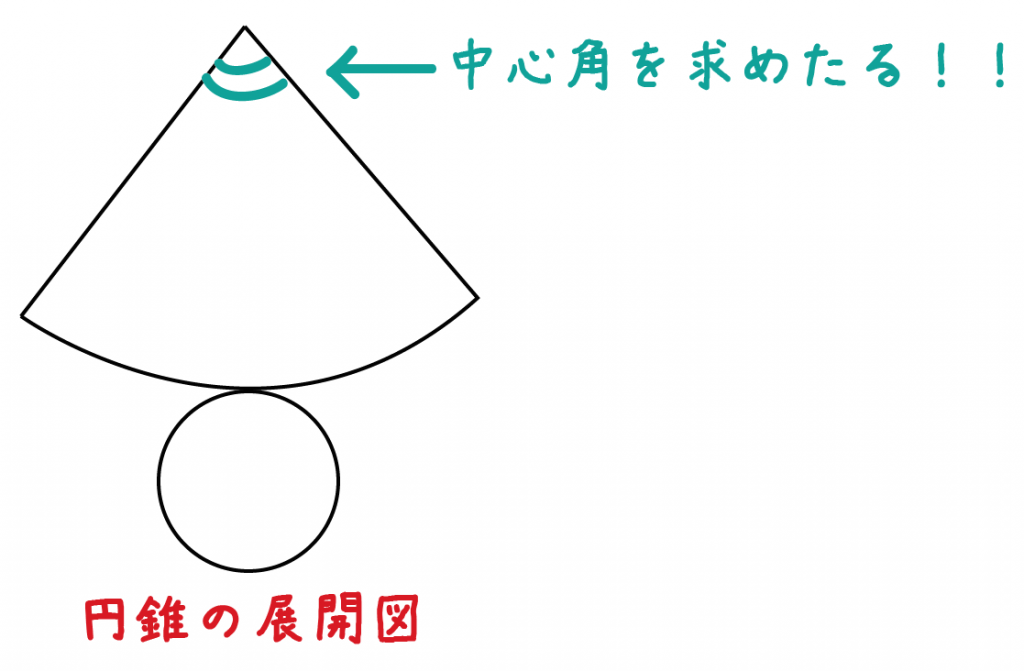



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
図オの円錐の表面積 この長方形を辺abを軸として1回転させてできる立体の表面積を求めなさい。 は,中学校3年生で習う三平方の定理が必要になります.まだ習っていない場合は,三平方の定理を習ってからやってください. 錐体の体積の求め方:底面積×高さ× 1 3 →底面積と高さの2つ要素が分かれば体積が分かる. →形が変形しても 底面積と高さが変化しなければ体積も変わらない. ①下図の3つの立体は同じ体積(底面積も高さも同じ) →底面積×高さ× 1 3 が成り立つ ②円錐の表面積の求め方は完全パターン化できる! だから、円錐の母線はつぎの線分ABになるってことだね。 もくじ• 扇形の面積を求めるには中心角が必要ですが大抵の場合、これが不明です。 母線を10㎝、半径を6cm、円周率を3




公式を図解 すい体の体積 円すいの表面積の求め方




球の表面積と体積の公式 数学fun
円錐の表面積を求める 展開したときのおうぎ形の中心角を求める それぞれの問題を解説していきます。 問題 下の図の立体についてそれぞれ求めなさい。 (1)この円錐を展開したときにできる側面のおうぎ形の中心角を求めなさい。 (2)この円錐の表面積を求めなさい。 体積や表面積を求める問題はよく目にすると思いますが その中でも円錐を取り上げた数学・算数 円錐の面積?の求め方。 上部は直径60cmの円で、下部は直径90cmの円。横面の線の長さは60cmの円錐を途中で切ったような横から見たら台形みたいな図形の側面積の求め方が分かりません。 質問no 三角形の面積の求め方なのですが、下の公式の証明を教えてください! 三角形ABCにおいて、 AB→=(a,b) AC→=(c,d)のとき、 面積S=1/2(adbc)←絶対値 よろしくお願いします!




円錐の表面積を簡単に求める方法 Easy Way To Find The Surface Area Of A Cone Youtube




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室
続いて表面積です。 円錐の表面積の公式は「底面積 側面積」でしたね。 底面積は6 × 6 × π = 36π とすぐに出せますね。 続いて、円錐の側面積の求め方は「半径 × π(半径 母線)」でしたね。 よって、側面積の式は 6π(6 10)= 96π となります。 円錐の側面積の公式 まずは、公式だけ図でさっと確認するよ つぎに、円錐の特徴を確認して、そのあとに側面積を求めていくよ 円錐の特徴 円錐の特徴は主に次の二つだよ 円すいの展開図、側面積の求め方! 公式を使って15秒で解こう♪ 面積 面積 この円すいの側面積を求めなさい。 円周率は314とします。 知りたがり




円すいの側面積の求め方 Youtube




円錐の表面積の求め方 公式と計算例
円錐の体積は、底面積×高さ×3分の1です。 円錐の表面積は、展開して扇形と円になるので、計算して足せばいいです。 扇形の面積の出し方は、 面積=2分の1×弧の長さ×半径です。 弧の長さは、2×π×半径×360分の角度です。 7人 がナイス! しています 円錐の側面積の求め方 解説編 円錐の側面積の求め方 今回は, 円錐の側面積の求め方 について 動画解説 しています。 所要時間は 7分 程度です。 円錐の側面積を簡単に求める式があるのですが,けっこう忘れやすいのですよね。 そこで,なぜその式が成り立つのかについて解説しています。 理由を知っていると,自分で式を導くことができるようになり,式を この図形の表面積を求めてください。 どうでしょうか? これは中学1年生の「空間図形」という範囲の 内容です。 なお、 『円錐の表面積の求め方』 で悩んでいる方は ↓こちらをご参照




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積の求め方 公式と計算例




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook
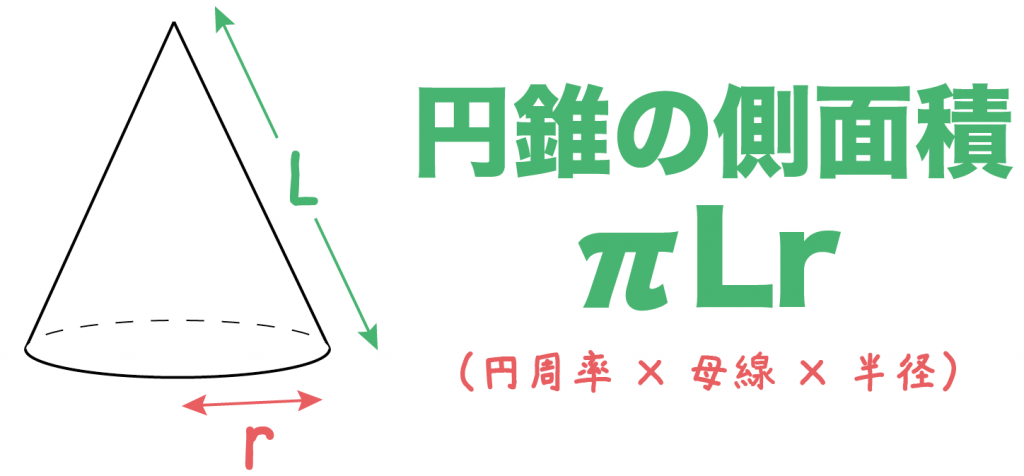



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




至急です の求め方が分からないです 詳しく教えてくれる Clear
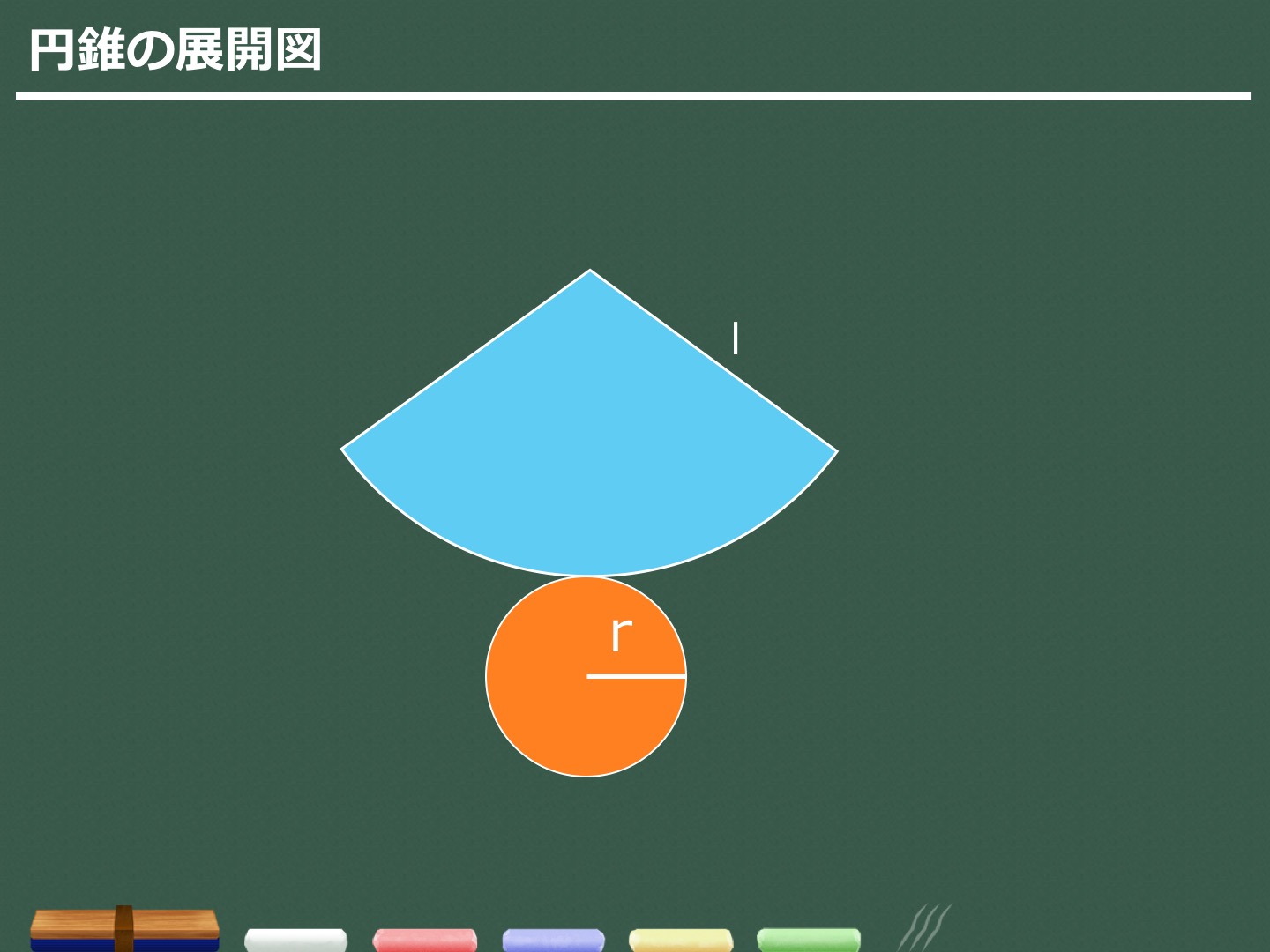



3分でわかる 円錐の体積 表面積の求め方 合格サプリ




円錐の表面積の求め方 You Look Too Cool




円すいの展開図 表面積の求め方 公式があるの知っていますか




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo



円錐の側面積の求め方が分かりません 図のような底面の半径が2cm 母線 Yahoo 知恵袋
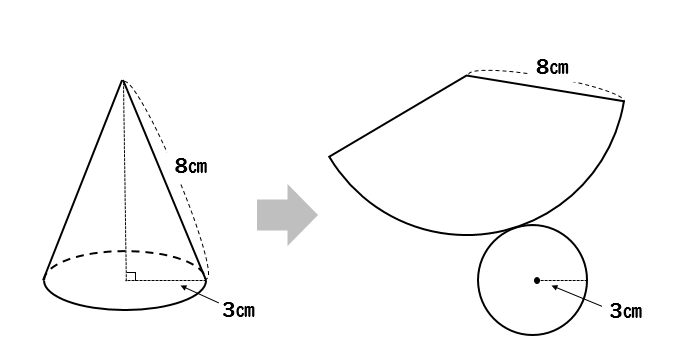



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
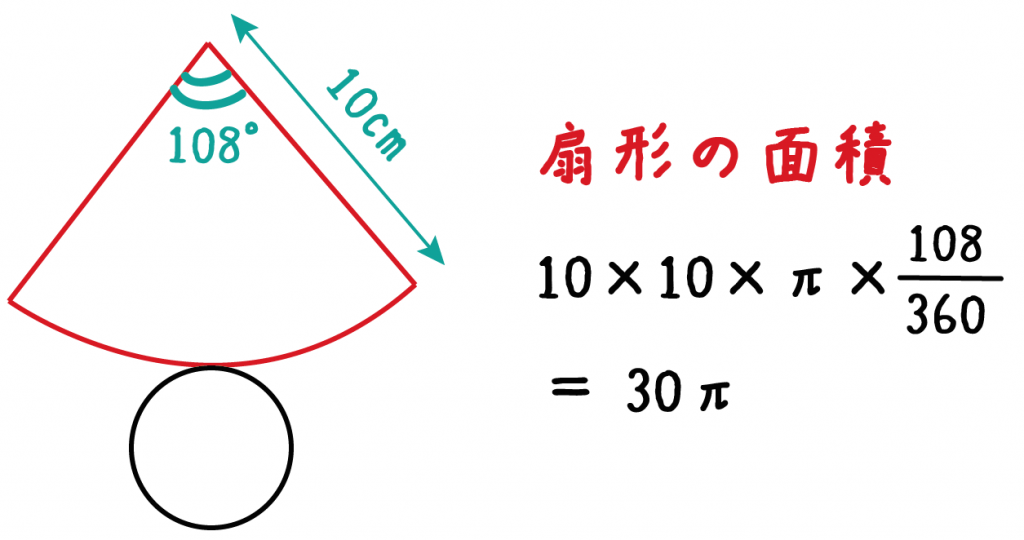



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




この円錐の表面積の求め方を教えてください Clear




Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ



円錐の体積と表面積の求め方を教えてください 錐の体積 1 Yahoo 知恵袋
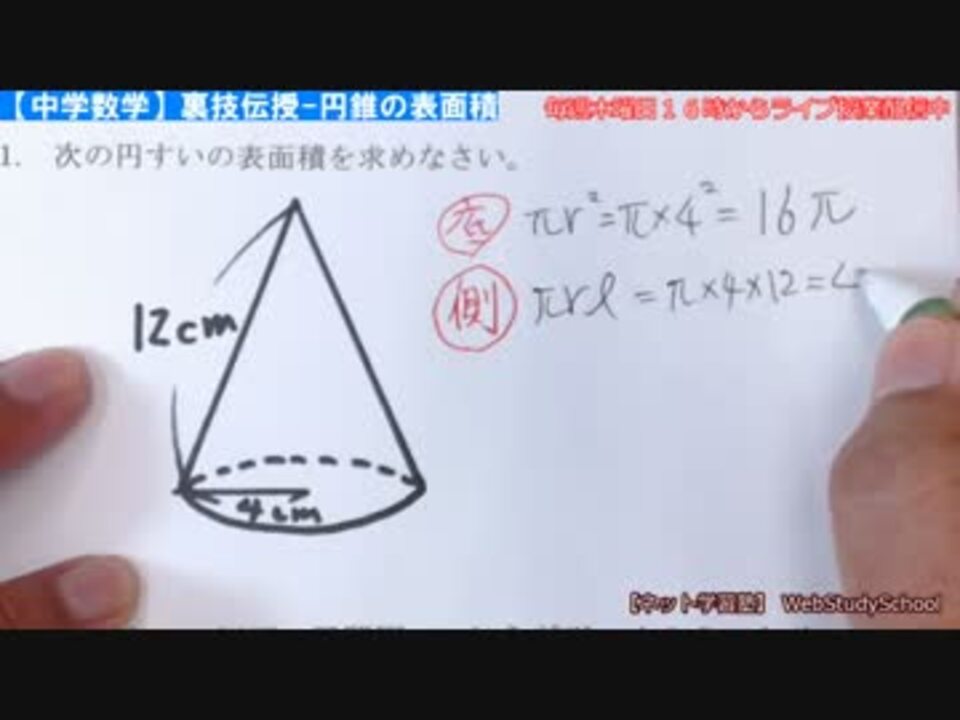



Hd限定円錐 体積 求め方 裏ワザ 最高のぬりえ
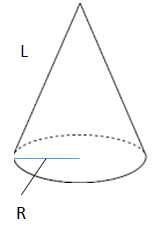



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー



1



1




角錐 円錐の体積と表面積の公式 数学fun




公式を図解 すい体の体積 円すいの表面積の求め方



円錐とは 体積 表面積の公式や求め方 受験辞典




公式を図解 すい体の体積 円すいの表面積の求め方




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




円錐の表面積 あんず学習塾のメモ 図表置き場




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト



底面積の求め方は 5分でわかる計算 円柱 円錐 四角柱 三角柱の底面積




円錐の体積の求め方 公式 小学生 中学生の勉強




毎日問題を解こう 27 苦手な数学を簡単に




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室



1




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題




円錐の表面積 Youtube




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
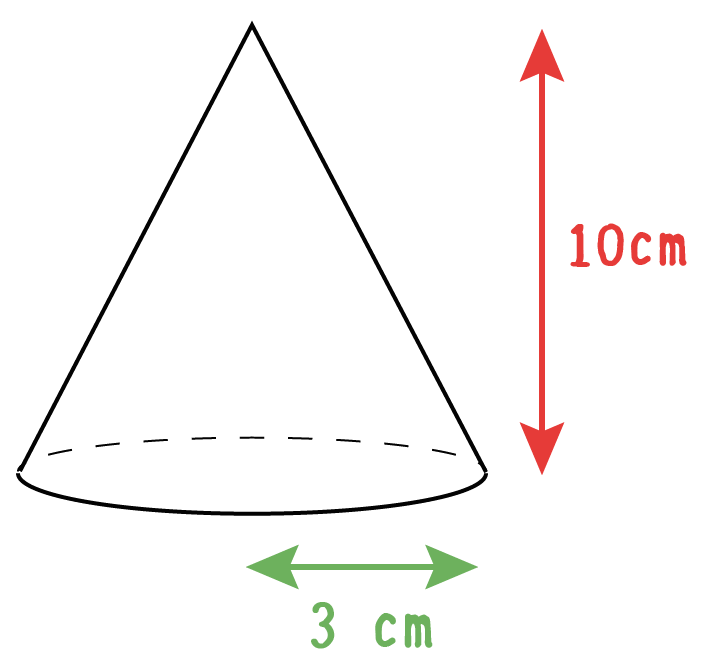



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




円錐台 Wikipedia




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 公式と計算例




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




高校入試対策数学 円錐に関する対策問題 Pikuu




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット
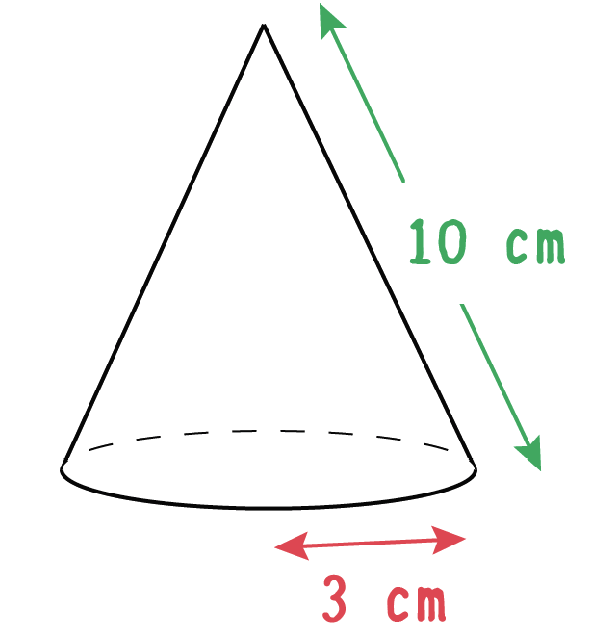



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ
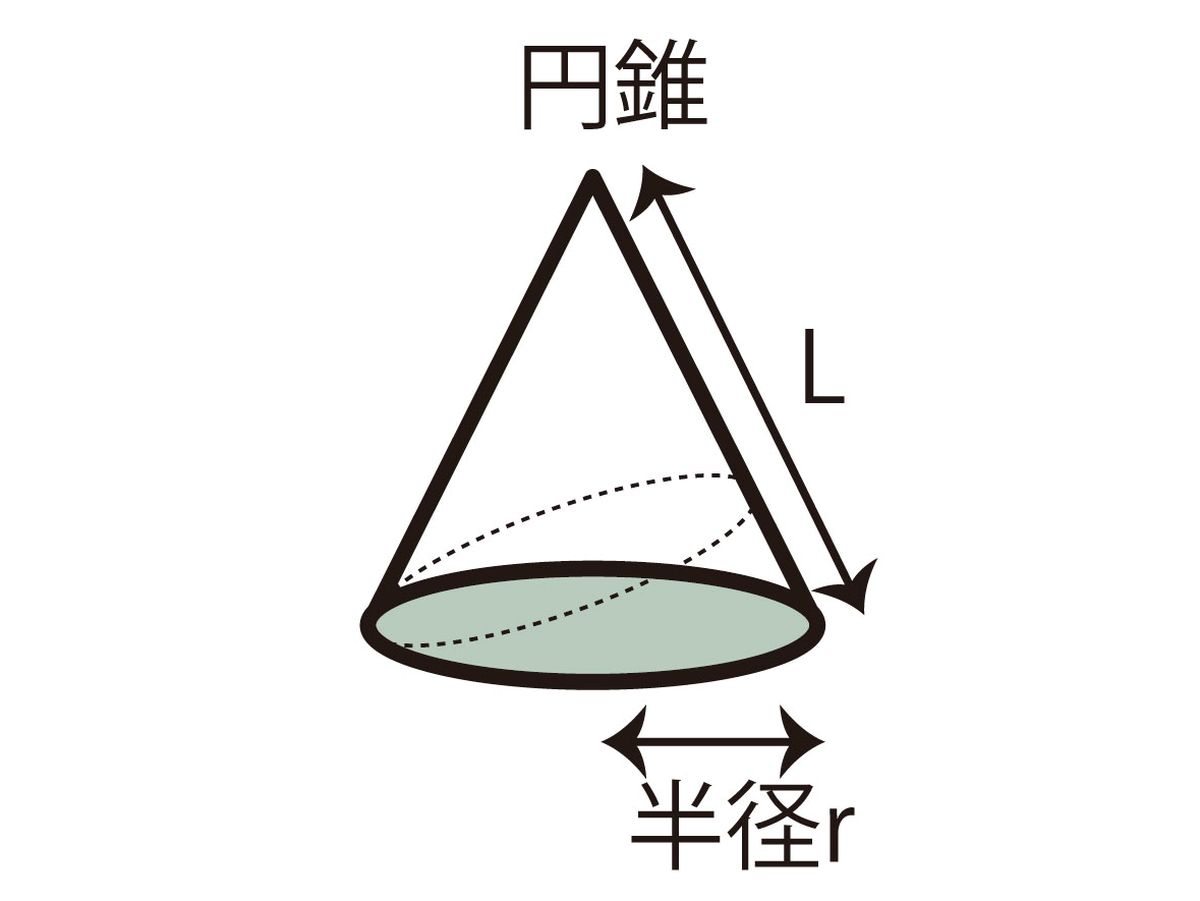



円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
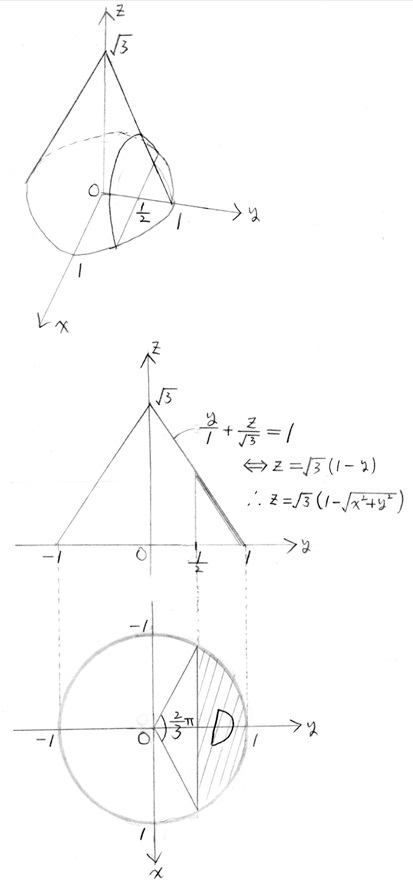



切った円錐 円柱の側面積の求め方 Den Of Hardworking
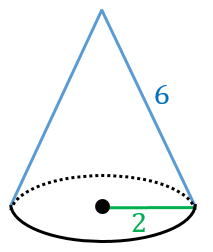



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円柱表面積公式 體積 表面積 Gkgnae




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




裏ワザ公式 円すいの側面積を一瞬で求める方法 Youtube




回転体 円錐の体積と表面積の求め方 現役塾講師のわかりやすい中学数学の解き方



図形 円錐の側面積の求め方 名古屋市北区の学習塾は思考力を育む 泰成スクール
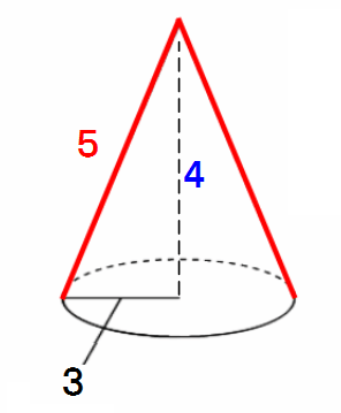



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo



円錐の側面積の求め方 インターネット家庭教師のアスミラ




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 公式と計算例




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積 Youtube




投影図から円錐の表面積を求める方法がわかりません 答えと解説を詳しく教えてください Clear




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の体積ってなんであの公式なの Webty Staff Blog
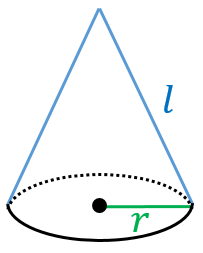



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




中1数学 円すいの側面積の求め方 Youtube



2 2 Abcd Ad Descubre Como Resolverlo En Qanda



1
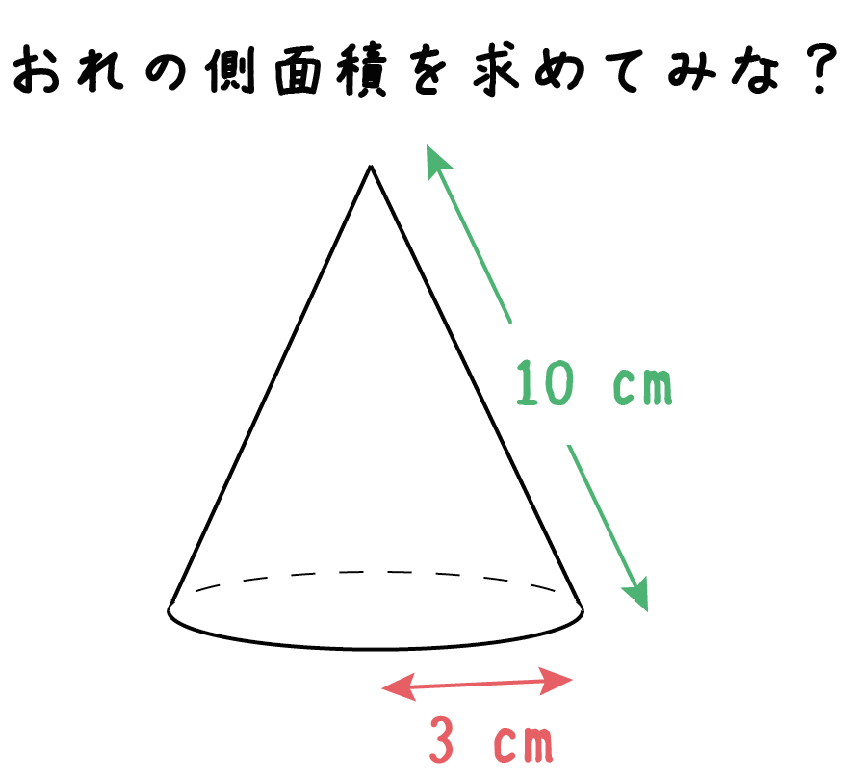



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題
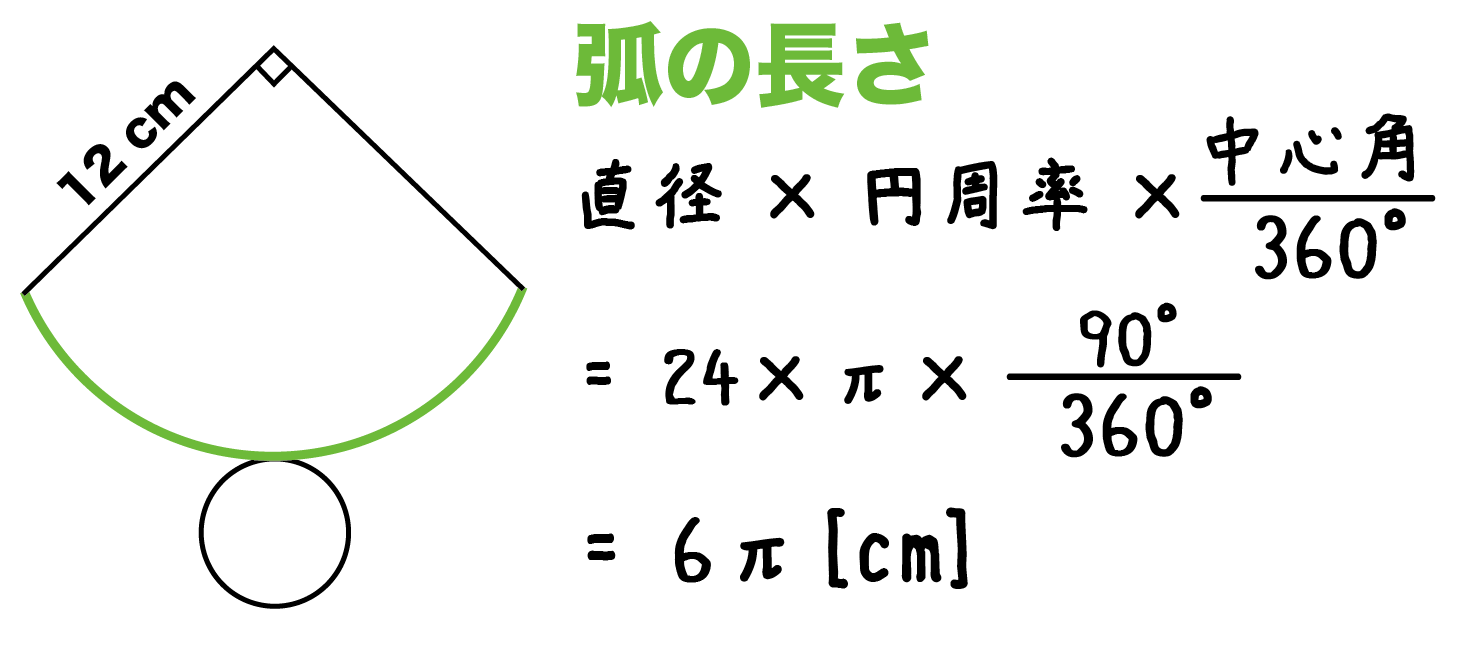



中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿