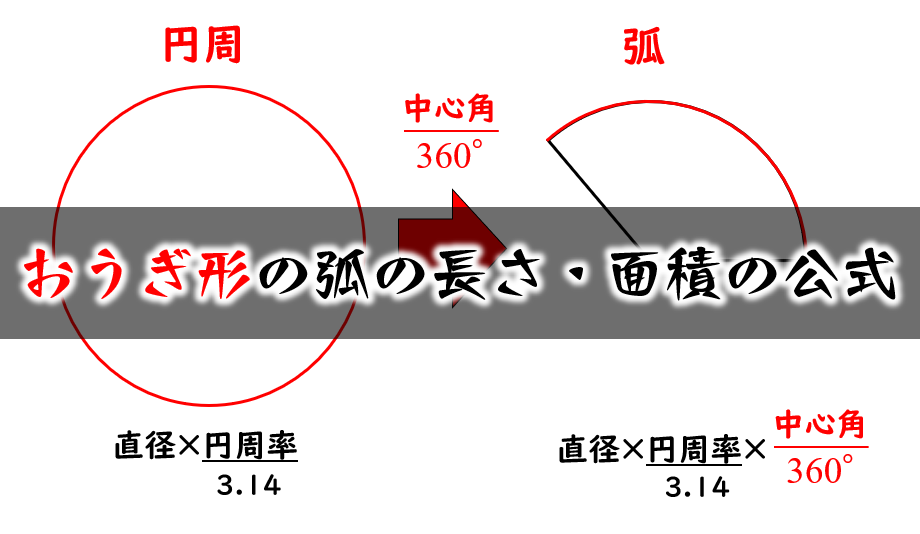
中心角の簡単な求め方教えてください! 上本 き形の中心久の求め方 しpro 半径5cm, 弧の長さご 4z cm のおうぎ形0 申訪角の大きさを求めます。 円とおうぎ形 中心角 簡単な 求め方 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こちらの記 弧の長さ=直径×円周率× 中心角 「 中心角 」は、円の中心角360°を全体としたとき、扇形の中心角がどのくらいを占めるかを表す割合です。

中心角の簡単な求め方教えてください Clear
中心角 求め方
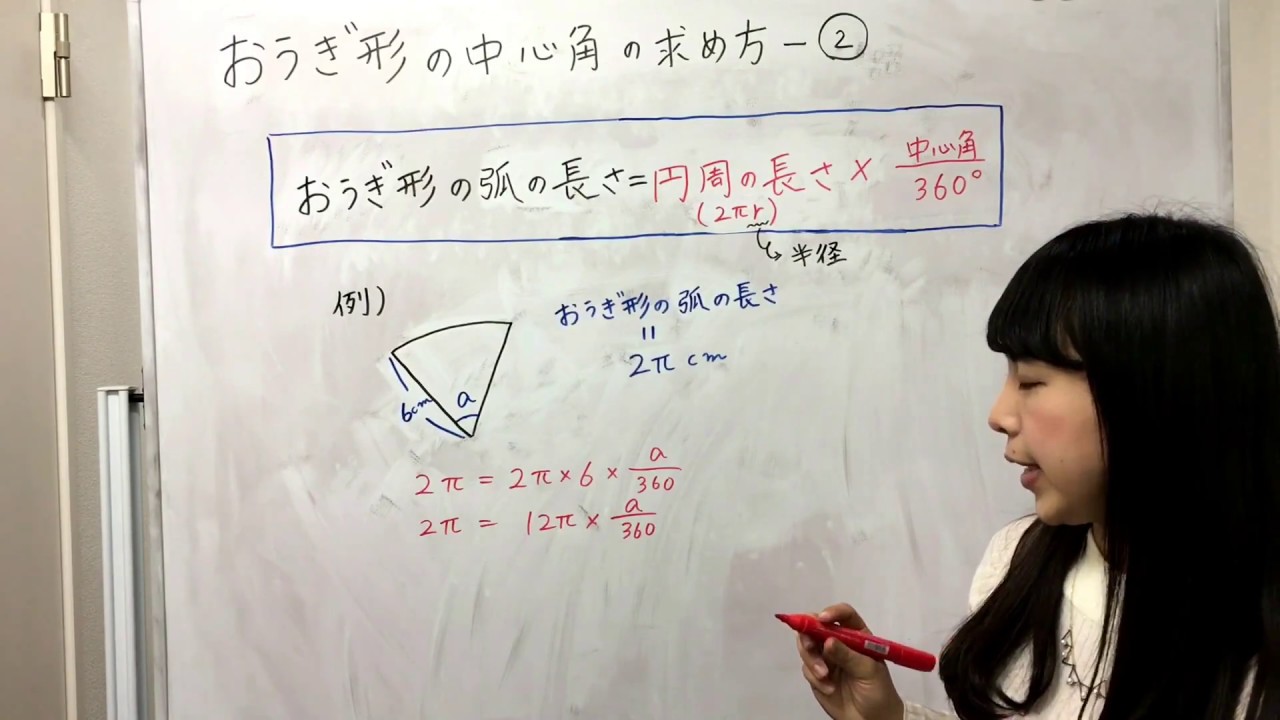
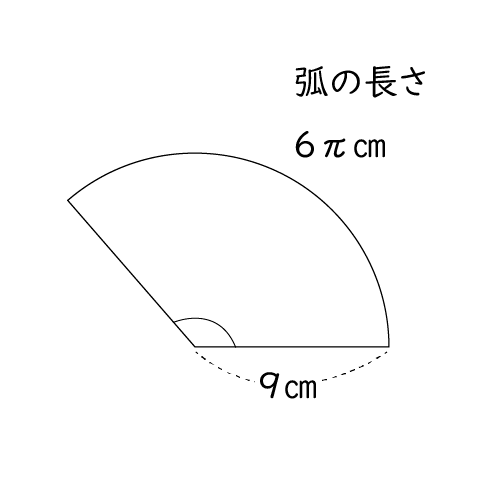
中心角 求め方- 単元:おうぎ型の中心角の解き方 問題 半径9㎝、弧の長さが6n㎝のおうぎ形の中心角を求めなさい。 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年~中学3年生内容計算の基礎養成演習時間割 円すい展開図・中心角の公式 の求め方 おうぎ形の弧の長さ L は L = R × 2 × 314 × θ 360 ∘ 式を変形して θ = の形にすると ① θ = 360 ∘ × L ÷ ( R × 2 × 314) ① また、底円の円周の長さ l は l = r × 2 × 314 L = l より、 L = r × 2 × 314 を ① ① に代入して θ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
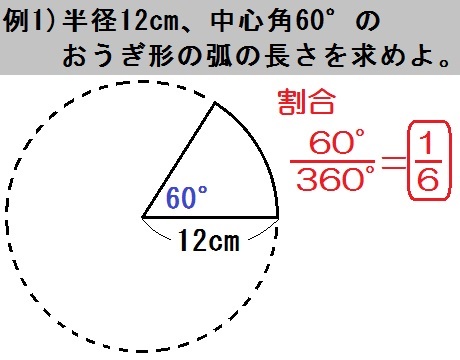
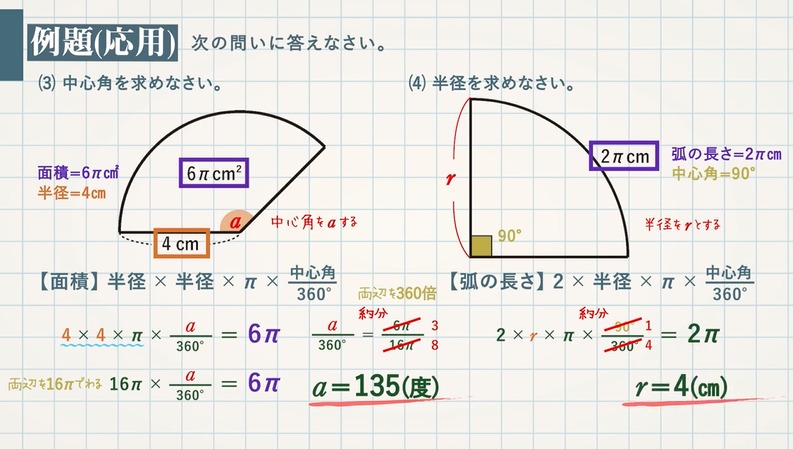
最も好ましい 扇形 中心角 求め方 公式 扇形 中心角 求め方 公式 扇形の中心角を求める公式 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ 公式は ちなみに、 中心角を求める公式 もあって 中心角 = 360× 半径 母線 中 心 角 = 360 × 半 径 母 線立体角の計算例 円錐の立体角は、 2 π ( 1 − cos θ 0) という公式で計算することができます。 ただし、 θ 0 は円錐の中心軸と母線がなす角度(平面角)です。 円錐の底面を円板をみなせば、「円板が張る立体角の公式」と言うこともできます。
>円すいの展開図で中心角がわからない時の弧の長さの求め方を教えてください。 わかっているのはおうぎがたの半径6センチと面積12π㎠です。お願いします。 中心角を求めてみよう。 中心角をxと置いて、面積に関する方程式を立てみて〜おうぎ形の中心角の求め方 まとめ おうぎ形の中心角を求める方法は大きく分けて3つのパターンがありました。 方程式を利用して求めるパターン;④No12以降の各中心杭までの弧長は、中心杭間距離000mを逐次加えて求め、それに対する偏 角は、中心点杭間距離に対する偏角δを、加えることにより求める。 例えば、No12の杭は、 ° ¢ ² ° ´ ´ = 5 43 57 314 180 2 m 000m δ= であるから、IPから
おうぎ形の中心角を求める問題で,わかっている数字が変わると求め方がわからなくなります。 ※ このQ&Aでは、 「進研ゼミ中学講座」 会員から寄せられた質問とその回答の一部を公開しています。円周を8等分した点です x, y, z の角度を求めましょう →1コマあたりの中心角は 360°÷8 = 45° xは3コマ分の中心角の半分 (=円周角) → x = 1 2 1 2 (3×45°) = 135 ° 2 同様に、円を6等分してできた扇形の弧の長さは、もとの円の円周の6分の1です。 ここまででなんとなく分かったかもしれませんが、扇形の弧の長さの求め方は扇形の面積の求め方とほぼ同じ。 もとの円の円周の長さの (中心角) になります。 つまり




1分でわかる 扇形の中心角の求め方 Youtube




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア
正四面体の中心角とは 正四面体では, 外心(外接球の中心) 内心(内接球の中心) 重心(位置ベクトルの平均) 垂心(頂点から対面に降ろした垂線の交点) は全て一致します。この点を「中心」と呼ぶことにします。面積の求め方 扇形 扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 また、2行目の l は扇形の 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
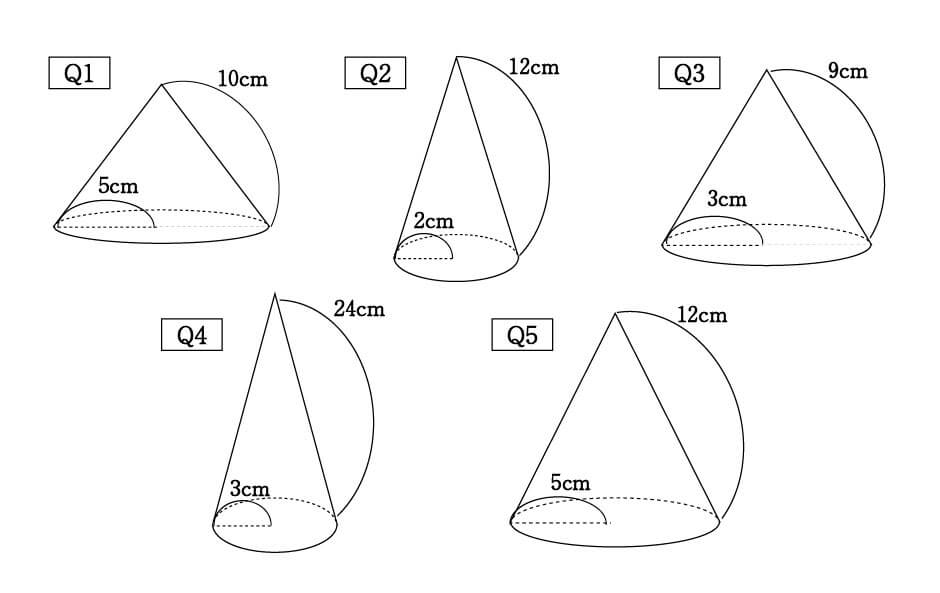
おうぎ形のうち,2つの半径にはさまれた角を 中心角 ,2つの半径をつなぐアーチ部分を 弧 といいます。 2ポイント『 底面の半径3cm、母線の長さ5cmの円すいの側面のおうぎ形の中心角を求めなさい。』 この問題も円すいを展開図にしてから考えます。 展開図にすると、オレン 中心角の割合が「\(\displaystyle \frac{\theta}{2\pi}\)」なので、\(2\pi\) が約分されてシンプルになりますね。 扇形の中心角の求め方 扇形の中心角を求めるには、先ほど説明した面積の公式または弧の長さの公式を利用します。




おうぎ形 半径の求め方 数学の記録




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ
扇形の作図・中心角・円周角 ⌛ 次におうぎ形について考えます。 結論からいうと、円すいを開いた時にできるおうぎ形の中心角は、母線と底面の半径の関係で決まってしまいます。 念のために、 公式に頼らない「扇形の中心角の求め方」をみていこう。 766 第6 章 中心力のもとでの運動 面積速度 時刻t に位置r にあった質点が,微小 時間後のtΔt にrΔr に移動したとする。 微小 時間Δt のあいだに位置ベクトルが掃いた面積ΔS は,r とΔr を2辺とする三角形の面積で近似でき る(図63)。 Δr の大きさをΔr と表し,r とΔr とのなす角を 底面の半径が3cmなので、円周=直径× π =6 πcm となります。 底面の円周とおうぎ形の孤の長さは等しいので、孤の長さも6 π cmです。 そこから、半径12cm&孤の長さ6 π cmのおうぎ形の中心角を逆算して求める──これが一般的な解き方です。



1




おうぎ形の中心角の求め方 Youtube
中心角92°が書いてあって,円周角が書いてないときは,92°÷2=46 ただし, ∠ BOA は図のように,優角(180°よりも大きい角)の方とする 《問題》 次の角度 x , y , z を求め数学1 平面図形 円とおうぎ形半径と弧の長さ,半径と面積から おうぎ形の中心角を求める。https//math7daifukublogspotjp/ 円の中心核の定義は、 「弧の両端を通る2つの半径の作る角」 でしたね。 この「2つの半径の作る角」のところは、②と③で確認した部分のことです。




中1 数学 空間図形9 おうぎ形の公式 17分 Youtube




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ
円周角の定理は 「円周角=½ 中心角」ですから、 ∠bac=½ ∠boc を示せばいいわけです。 oからbに補助線を引いて、大きさが同じ角に印をつけてみましょう。 注意すべきなのは、oは円の中心であり、a,b円周上の点であるため、oa=obであることです。数学・算数 扇形の中心角と円弧の求め方 扇形の中心角と円弧の求め方を教えて下さい(~_~;) 双方わからない状態です。(半径はわかります) 質問No 円周角の定理と証明、中心角の求め方を詳しく解説! 今回は数学が嫌いな人でも理解できるように、円周角の定理について工学博士が解説します。 まずは定理を解説して、その証明を解説します! 円周角の定理は試験でも使うことが多いですよ




扇型の求め方や中心角の求め方も分からないので 解説もお願いします この問題の答えは Clear




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる
目次 平面図形の面積の求め方の公式 台形=(上底+下底)×高さ÷2 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 円周=直径×円周率(314)=半径×2×円周率(314) 円の面積=半径×半径×円周率(314) おうぎ形の弧の長さ=円周×中心角/360そして、この角度はrad(ラジアン)という単位で表す。このとき、半径r、中心角θradに対する弧の長さはrθとなる。 360°法との関係は、半径1の円の円周が2πで、その中心角が2π(rad)なので 360°= 2πrad 180°= π rad 90°=1/2πrad 60°=1/3πrad 45°=1/4πrad それじゃぁ、扇形の中心角について学んでいこう! 今回の記事では扇形の中心角を求める方法について解説していきます。 中心角を求める方法には何パターンかのやり方があります。 どのやり方が自分に合ってるかを考えながら、解法を身につけていき



中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube




おうぎ形 弧の長さ 面積 中心角の求め方 学習内容解説ブログ
中学数学円錐の中心角の求め方3パターン なぜか 三平方の定理円錐の高さが??体積を求める問題を解説 円錐の体積の求め方 公式と計算例 Scipursuit;おうぎ形の公式 弧の長さ = 円周 × 中心角 360° 中 心 角 360 ° = 直径×314 × 中心角 360° 中 心 角 360 ° おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時に円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
扇形 ~弧の長さ、半径から中心角を求める~ 実行数 本ライブラリは会員の方が作成した作品です。 内容について当サイトは一切関知しません。問題側面のおうぎ形の中心角の大きさを求めなさい。 側面のおうぎ形は半径 $5 \rm cm$ の 円の一部 といえます。よって、 円周と弧の長さの比率 から、おうぎ形の中心角を求めることができます。 半径 $5 \rm cm$ の円周なので、$2×5×π=\textcolor{blue}{10π}$ おうぎ形弧の長さ・面積・中心角の求め方 21年2月1日 学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ 学習内容解説ブログをご利用下さりありがとう




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



おう ぎ 形 の 面積 求め 方




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




円錐の側面積 展開図の扇形の中心角 半径 母線を軸として解く 身勝手な主張
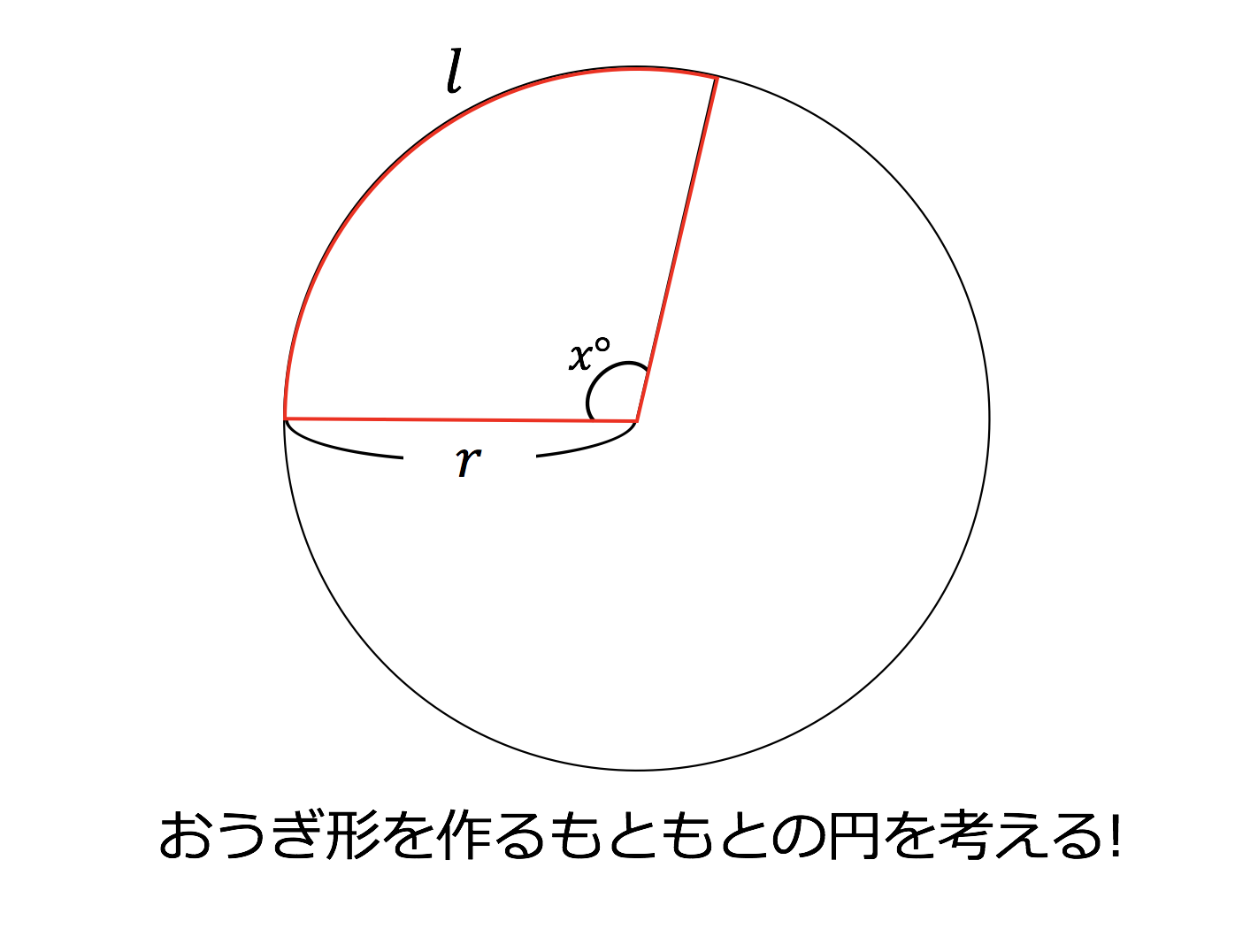



3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




中学数学 円錐の中心角の求め方 3パターン なぜか分かる はかせちゃんの怪しい研究室




扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち




扇形 の 面積 の 求め 方 小学生 かわいいドラえもん




扇形の中心角の求め方を教えてください Clear



印刷可能 円錐 中心角 求め方 比



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest
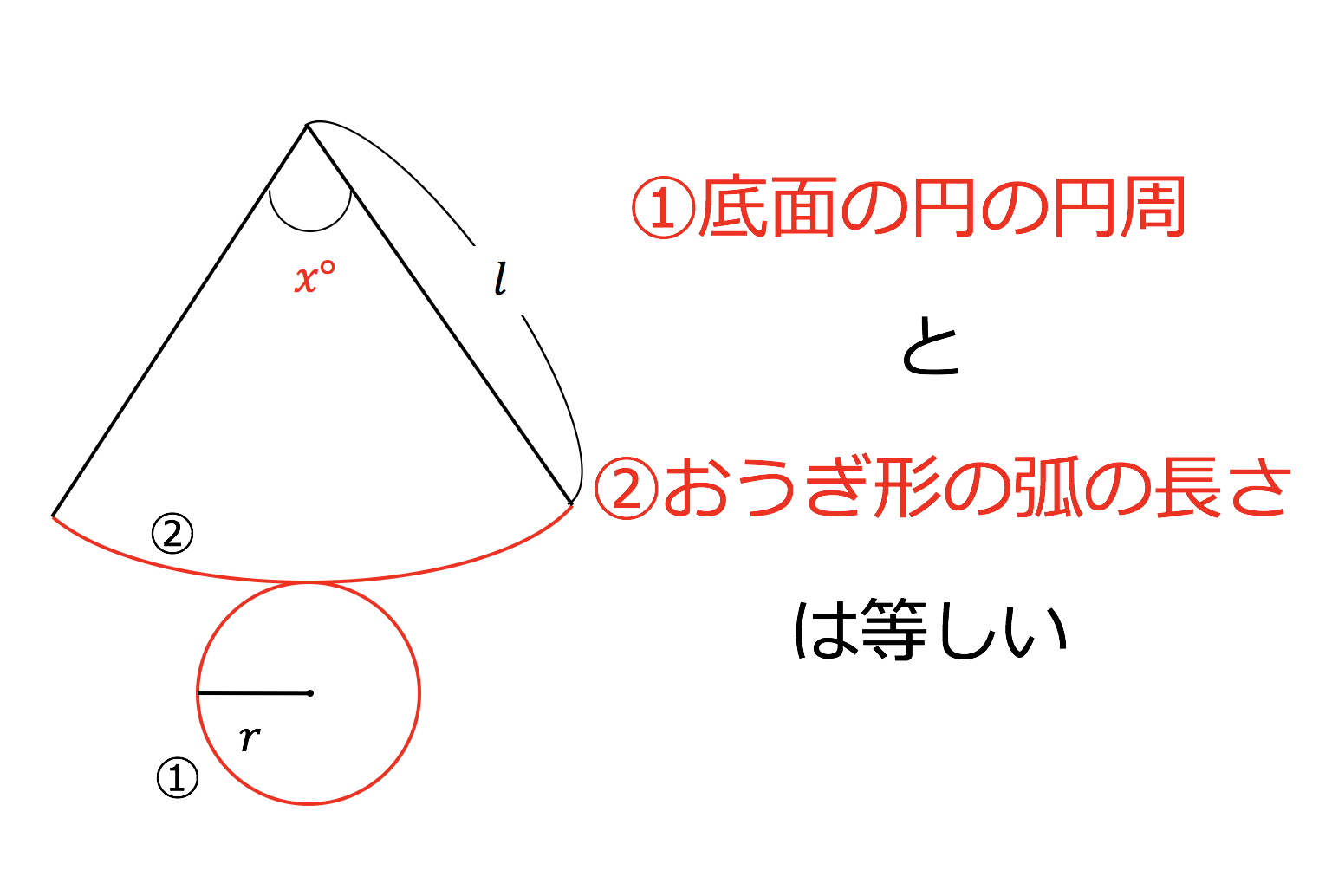



3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




半径6cm 面積18pcm の扇形の中心角の求め方を教えて欲しいです Clear




おうぎ形 中心角の求め方を公式を用いて解説するぞ Youtube




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト




中心角の簡単な求め方教えてください Clear




中心角を求める計算方法を教えてください 弦長lと半径rが与えられた 数学 教えて Goo




中3数学 円周角の定理を使った定期テスト予想問題 Pikuu



1




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張




中心角の簡単な求め方教えてください Clear



Q Tbn And9gcsgrcnoenhh Hwfhkmfhztuzoleuglrrcmjplt8d 4u Vhwpxwo Usqp Cau



中学1年生数学 おうぎ型の中心角の求め方 長野地区 Itto個別指導学院 長野市の学習塾




扇形 中心角 公式 学び 教科書 わかる




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




おうぎ形の中心角の求め方を詳しく教えてください お願いします Clear



中心角40度 弧の長さ2pcmの扇形の面積中心角30度 弧の長さpcmの扇形 Yahoo 知恵袋




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1です お願いがあります 扇形の中心角の求め方を Clear




高校入試対策数学 円錐に関する対策問題 Pikuu



中学数学 平面図形 のコツ 円とおうぎ形




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ



半径10センチ 中心角90 の扇形oabの内部にoa Obを直径と Yahoo 知恵袋



側面のおうぎ形の中心角の求め方を教えてください 側面積の求め方はわかったのです Yahoo 知恵袋



おうぎ形まとめ 弧と面積の求め方 教遊者




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ



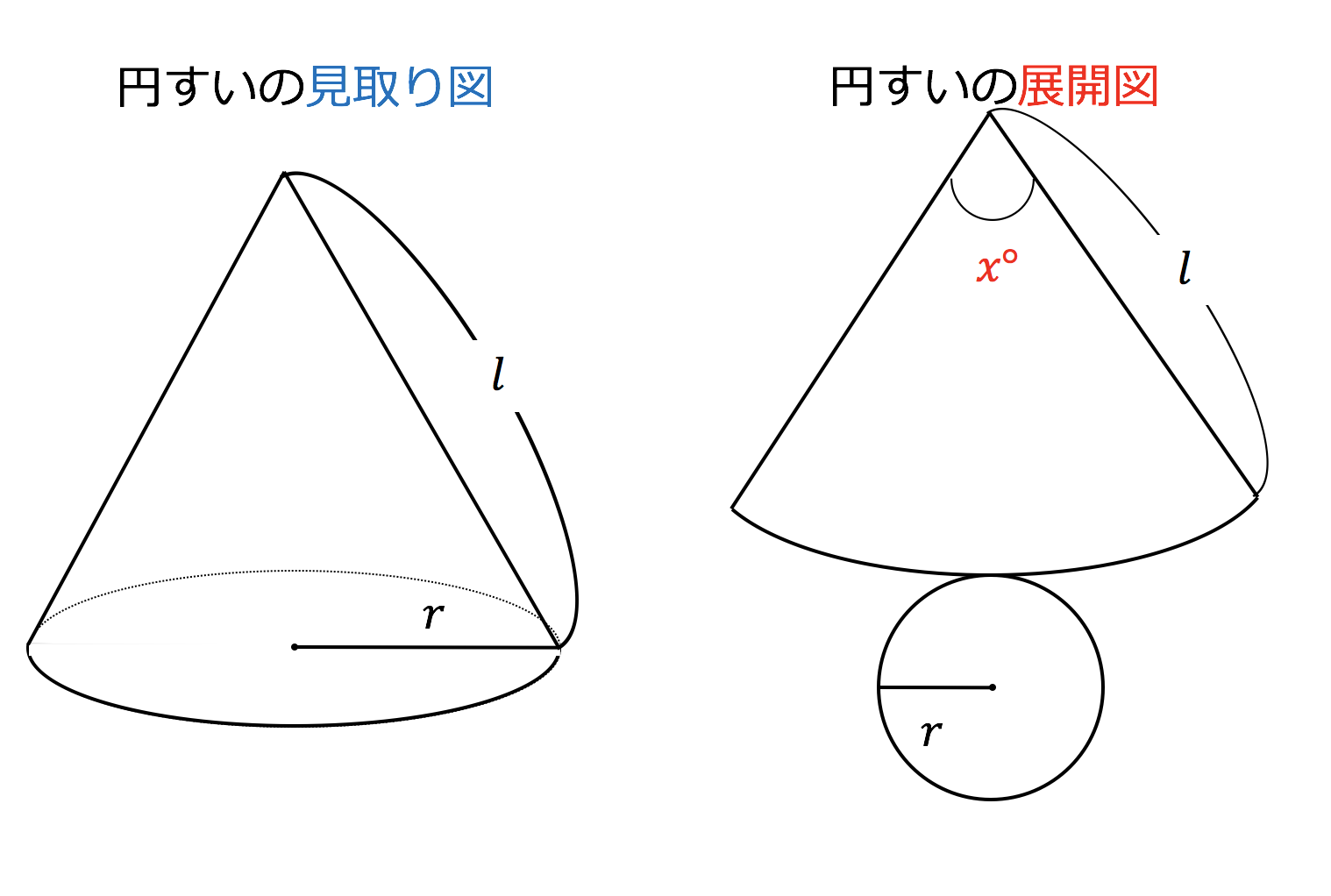
円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




公式を図解 すい体の体積 円すいの表面積の求め方



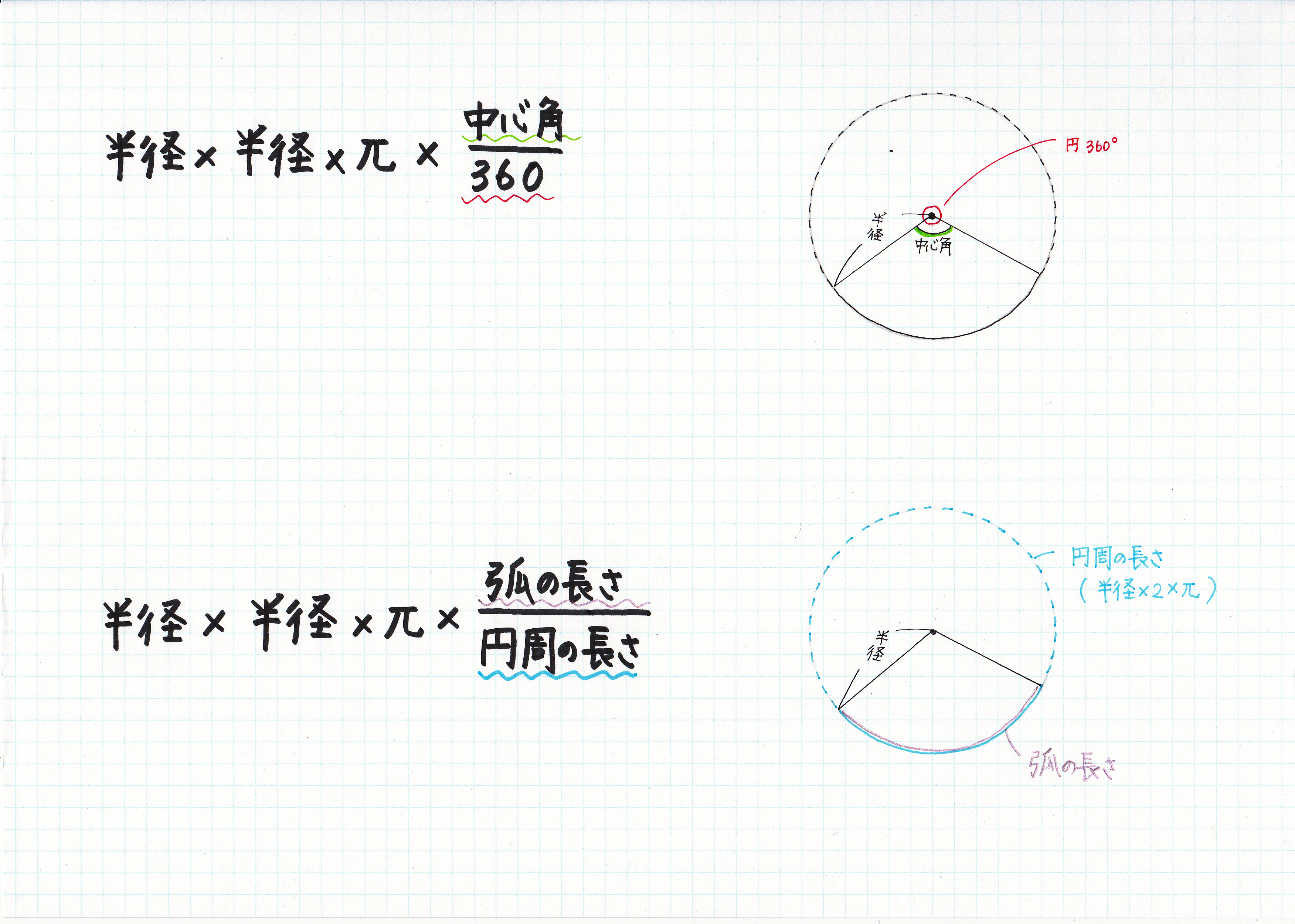
3




扇形の面積の求め方 公式と計算例




中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ




中学数学 おうぎ形の中心角を求める問題 Youtube




おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ



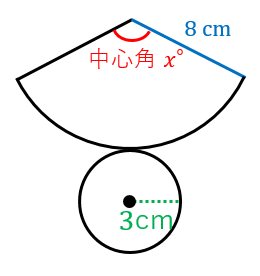
おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方




中学数学 扇形の中心角の求め方3パターン ピザでわかる なぜか分かる はかせちゃんの怪しい研究室




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
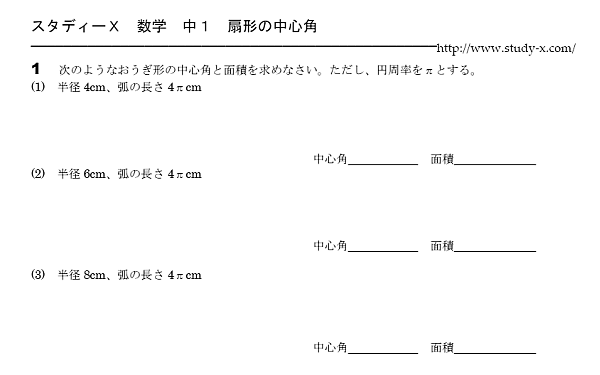



中1 数学 無料学習プリント教材




中1数学 おうぎ形の中心角の求め方 について ひっそりと物理や数学を解説する




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube




円 扇形 の面積 周や弧の長さの公式 数学fun




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




Kelas 7 Catatan Tentang 中1 数学 範囲 Clear



円錐の側面であるおうぎ形の中心角を求める問題 バカでもわかる 中学数学




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




中心角の求め方 Youtube



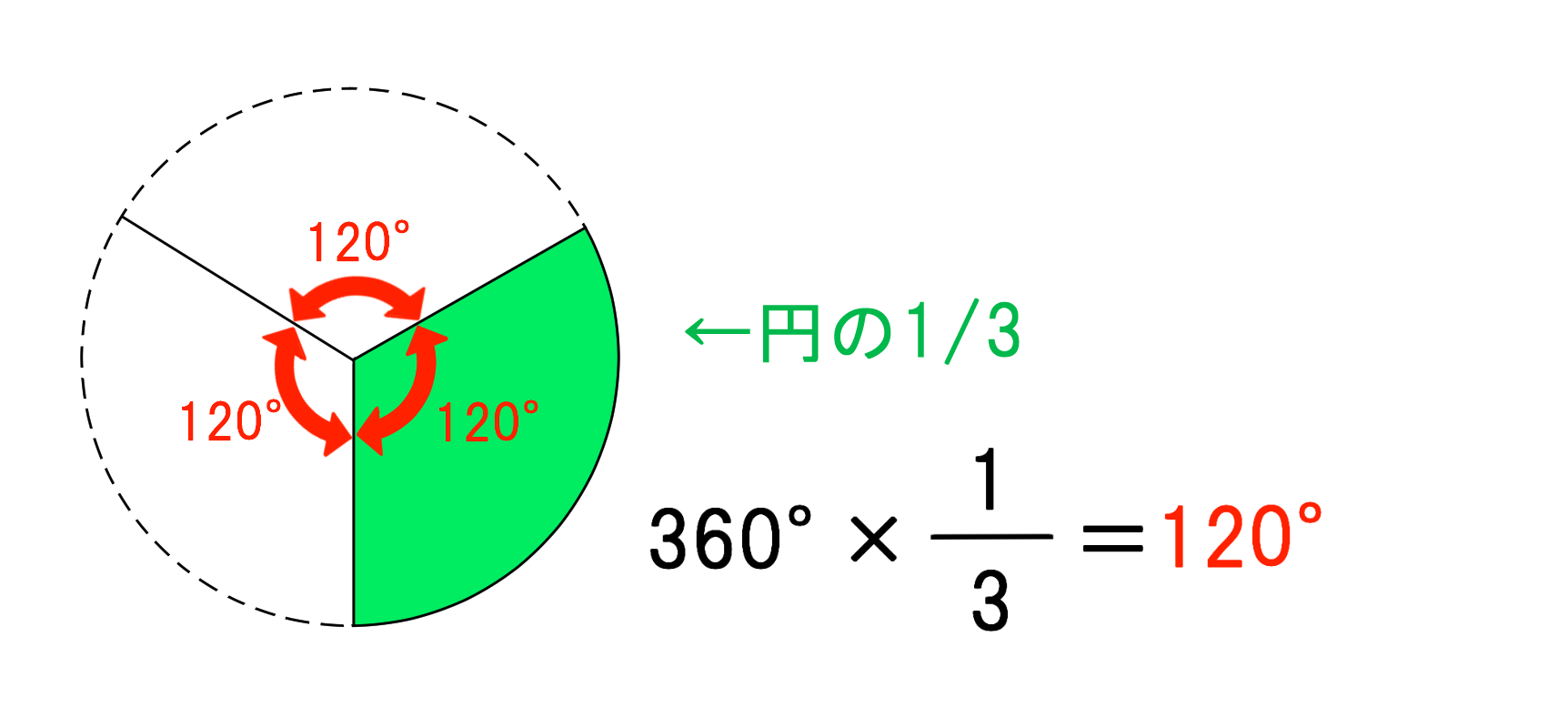
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




7 Times2 Descubre Como Resolverlo En Qanda




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
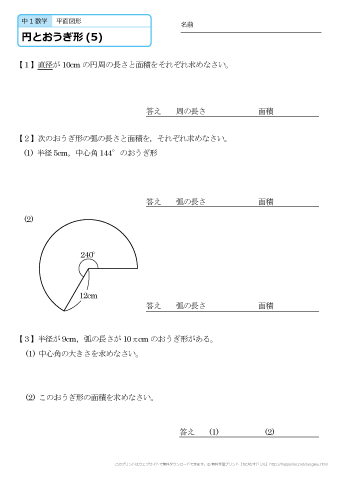



中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




中学数学 弧の長さから中心角や面積を求める Youtube
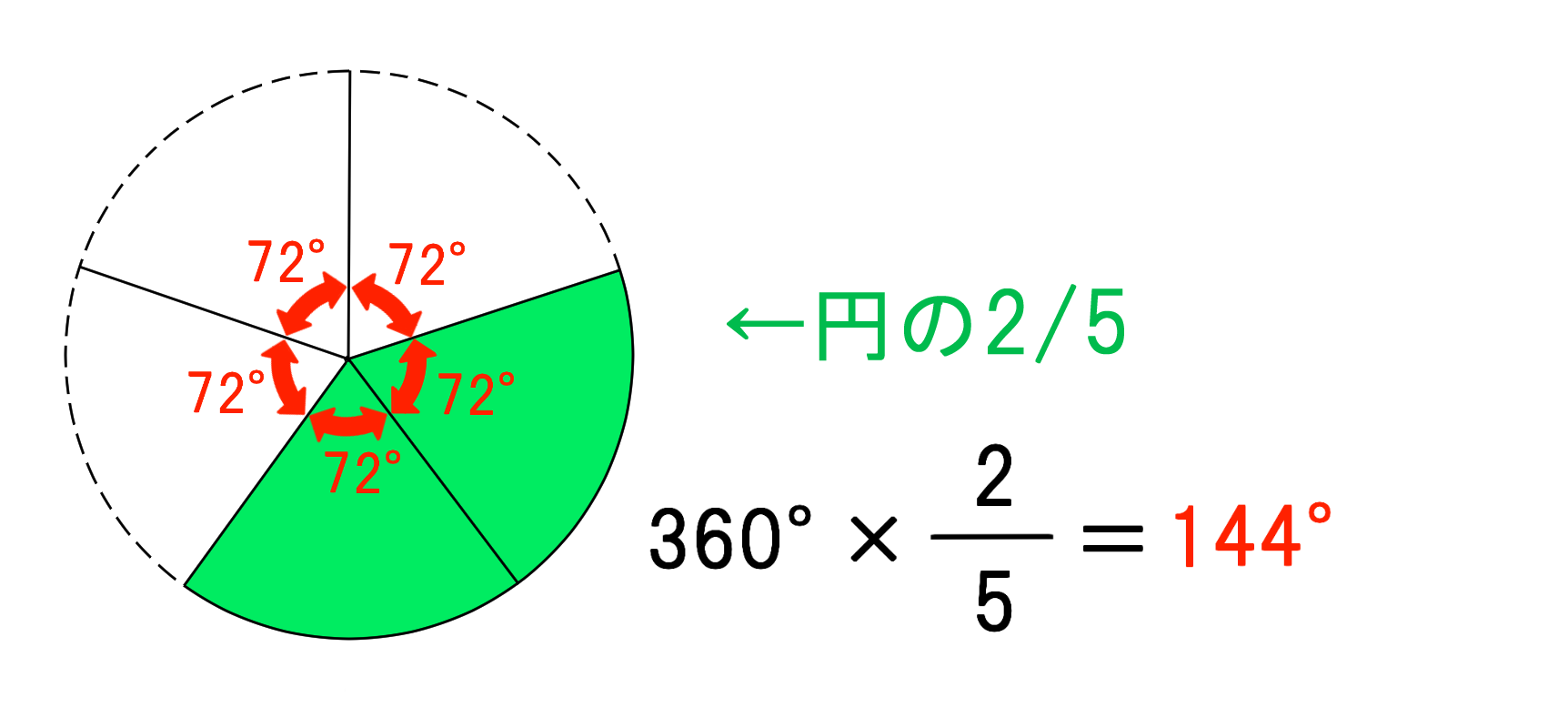



円錐の側面であるおうぎ形の中心角を求める問題 バカでもわかる 中学数学
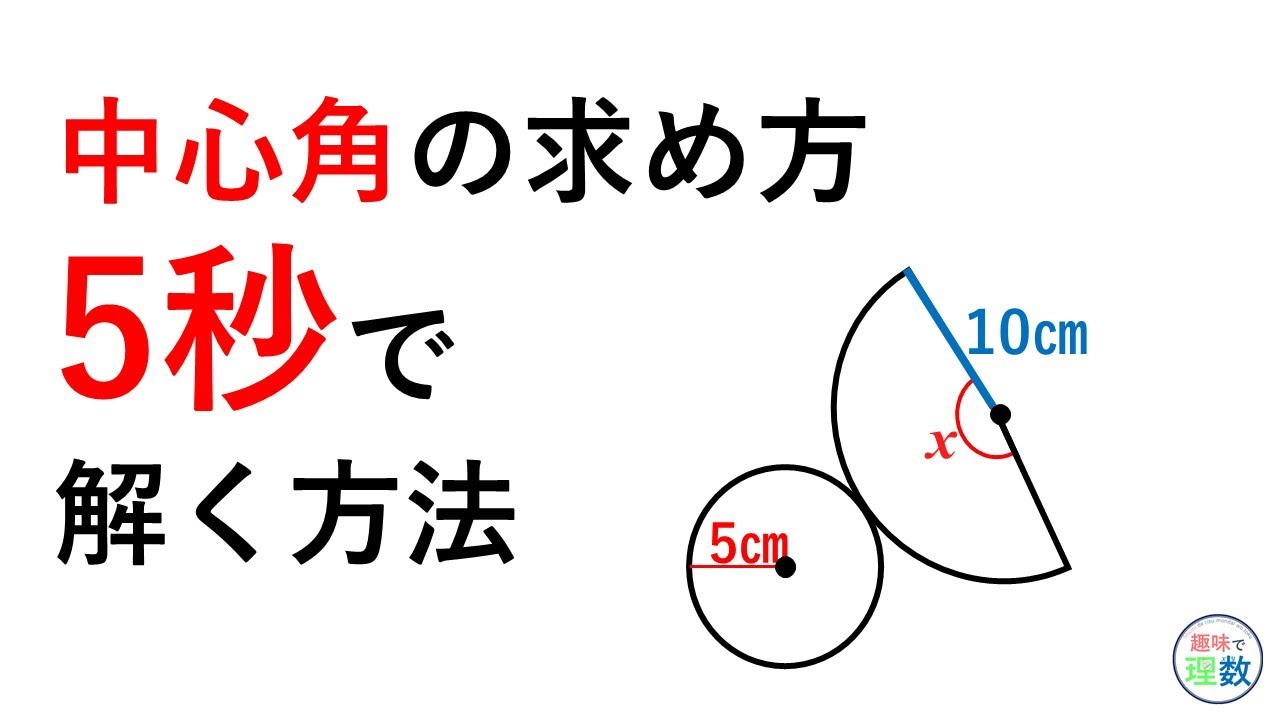



おうぎ形の中心角の求め方 Youtube




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学



弧




Study 円錐の側面 扇形 の中心角の求め方 中2数学 ちくらっぽインク




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
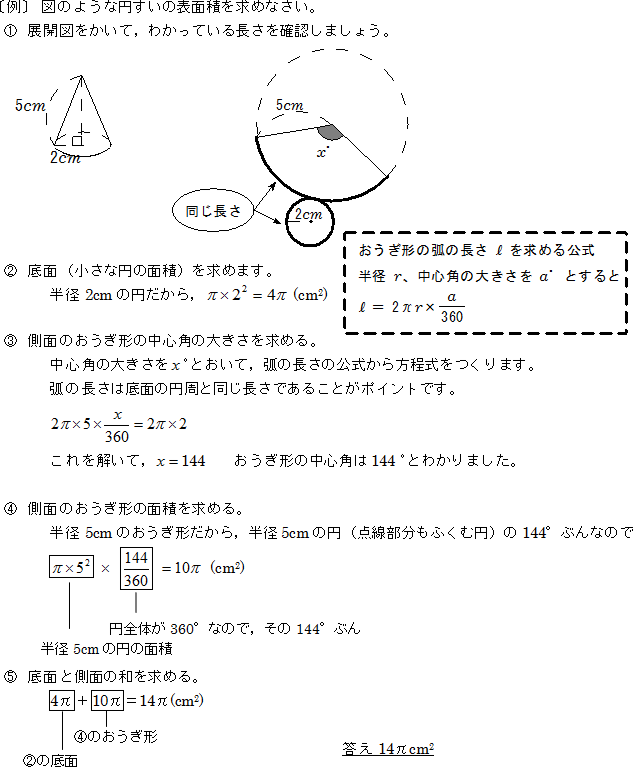



空間図形 円すいの表面積の求め方 中学数学 定期テスト対策サイト




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿